Probability Blog

This post looks at an application of probability within Machine Learning through the analysis of a data set.
Machine Learning
Probability
Logistic Regression
Confusion Matrix
Author

Shardul Dhongade

Published

November 28, 2023

Background

This blog post looks at probability within Machine Learning, and how it is used with algorithms like Logistic Regression to analyze data sets. This blog will look at analyzing a voting patterns of two parties in the US Government’s House.

Setup

We will first begin by checking our python version and importing the necessary libraries for this. We will use Pandas to read the csv file and manipulate its data, and matplotlib’s pyplot to display graphs and plot our data. Scikit learn (sklearn) libraries will also be imported for its metrics and models. We will use the metrics to see how accurate the model is and build a confusion matrix. The model libraries will be used to build the Logistic Regression and also split the data.

import sys

#Project requires Python 3.7 or above
assert sys.version_info >= (3, 7)

# Import libraries
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

Data

Let’s start by seeing what our data looks like.

# Read data
data = pd.read_csv("house_votes.csv")
data.head()
Class Name handicapped-infants water-project-cost-sharing adoption-of-the-budget-resolution physician-fee-freeze el-salvador-aid religious-groups-in-schools anti-satellite-test-ban aid-to-nicaraguan-contras mx-missile immigration synfuels-corporation-cutback education-spending superfund-right-to-sue crime duty-free-exports export-administration-act-south-africa
0 republican n y n y y y n n n y ? y y y n y
1 republican n y n y y y n n n n n y y y n ?
2 democrat ? y y ? y y n n n n y n y y n n
3 democrat n y y n ? y n n n n y n y n n y
4 democrat y y y n y y n n n n y ? y y y y

The dimensions of the data is (435, 17). There were 16 different issues for which voting in the House of Representatives was conducted, and 435 representatives voted. However, in the data set we can see some votes listed as ‘?’. This indicates that a vote was not given. We can now see how the data is structured and the way votes were provided.

Plotting the Data

Let’s plot the data to visualize what the distributions look like and see if we can draw any initial inferences from what we see.

First, let’s look at what the voting distribution actually looked like. While we have all the votes, it is difficult to see how many votes for yes/no/? were actually recevied in each category. Let’s first create a table to display this information.

# Display data distribution
df = pd.DataFrame([], columns=['Yes', 'No', "?"])
for col in data.columns[1:]: # '1:' to skip first column (Class Name)
    vals = []
    yes = data[col].value_counts()['y']
    no = data[col].value_counts()['n']
    na = data[col].value_counts()['?']

    vals.append(yes)
    vals.append(no)
    vals.append(na)

    df.loc[col] = vals

#Visualize df vote distribution
df
Yes No ?
handicapped-infants 187 236 12
water-project-cost-sharing 195 192 48
adoption-of-the-budget-resolution 253 171 11
physician-fee-freeze 177 247 11
el-salvador-aid 212 208 15
religious-groups-in-schools 272 152 11
anti-satellite-test-ban 239 182 14
aid-to-nicaraguan-contras 242 178 15
mx-missile 207 206 22
immigration 216 212 7
synfuels-corporation-cutback 150 264 21
education-spending 171 233 31
superfund-right-to-sue 209 201 25
crime 248 170 17
duty-free-exports 174 233 28
export-administration-act-south-africa 269 62 104

This is better to look at the overall voting spread of each category. After a first glance, it appears that most category had more ‘yes’ votes, indicating that in favor of the bill or issue passed was more likely.

Let’s display this on a stacked bar graph to see how the spread looks on a plot. We will also store the vote result in a list. This will be used later when we want to compare the winners. The list will be in left to right order of the categories provided.

# Plot data on stacked bar graph
df.plot.bar(stacked=True)
win_vote = ['No', 'Yes', 'Yes', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No', 'No', 'Yes', 'Yes', 'No', 'Yes']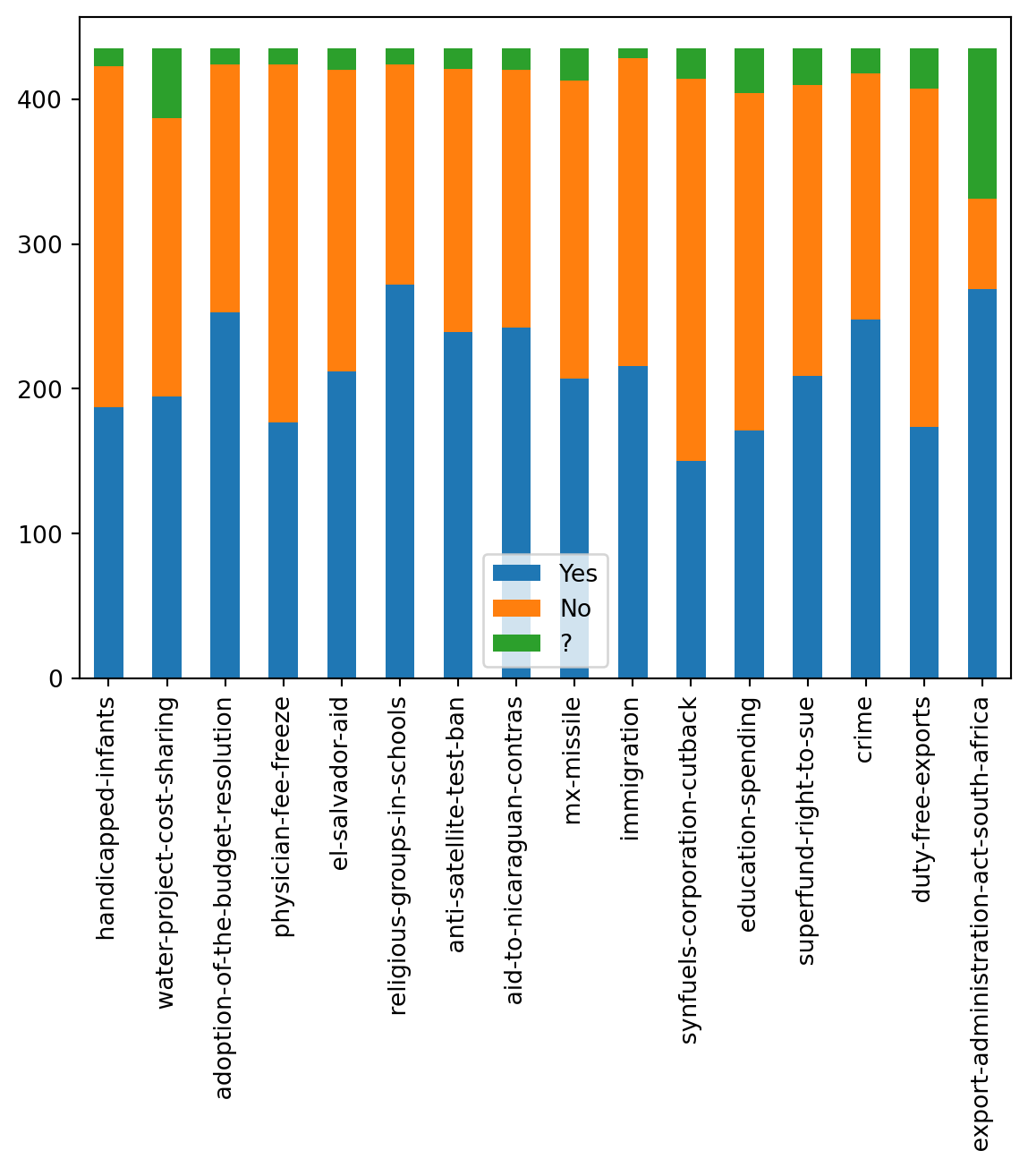

Let’s look at party specific data now. We know that two parties, the Republicans and Democrats, were present in voting. Let’s see how many members from each party are present.

# Look at party specific data, who voted yes/no in each category
print("Republicans: ", data['Class Name'].value_counts()['republican'])
print("Democrats: ", data['Class Name'].value_counts()['democrat'])

labels = ['Republicans', 'Democrats']
plt.pie(data['Class Name'].value_counts(), labels=labels, autopct='%1.0f%%')
plt.show()
Republicans:  168
Democrats:  267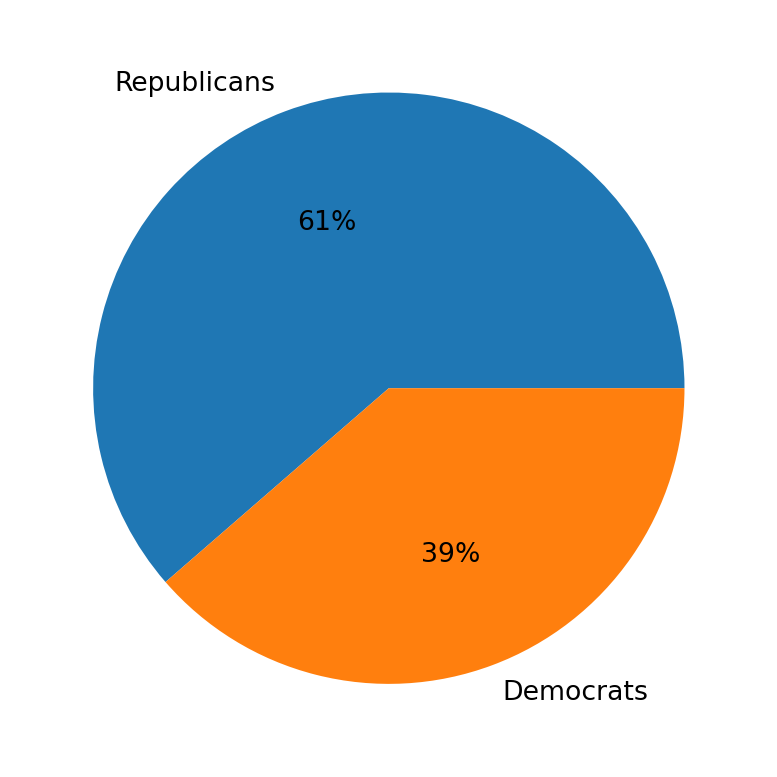

There are more Democrats present than Republicans. This is important information as it could indicate one party had stronger voting power, which may have played a role in which party got its favored outcome for each bill passed.

Let’s take each issue, and split it amongst the voting distribution for both parties. We can look at this and see which party got the favorable outcome. This will be done using the pivot table method which will build the table per each column against the Class Name. We will also use the win_votes list to add to the table as we go through the columns.

# Find number of wins for each voting issue per party 
df2 = pd.DataFrame(data)
i = 0 # Go through winning votes
for col in data.columns[1:]: # 1: Skips class name
    table = df2.pivot_table(index='Class Name', columns=col, aggfunc='size', fill_value=0)
    table['Winning Vote'] = win_vote[i]
    table.at['republican', 'Winning Vote'] = 'NA' #Format, remove from last
    display(table)
    i = i + 1
handicapped-infants ? n y Winning Vote
Class Name
democrat 9 102 156 No
republican 3 134 31 NA
water-project-cost-sharing ? n y Winning Vote
Class Name
democrat 28 119 120 Yes
republican 20 73 75 NA
adoption-of-the-budget-resolution ? n y Winning Vote
Class Name
democrat 7 29 231 Yes
republican 4 142 22 NA
physician-fee-freeze ? n y Winning Vote
Class Name
democrat 8 245 14 No
republican 3 2 163 NA
el-salvador-aid ? n y Winning Vote
Class Name
democrat 12 200 55 Yes
republican 3 8 157 NA
religious-groups-in-schools ? n y Winning Vote
Class Name
democrat 9 135 123 Yes
republican 2 17 149 NA
anti-satellite-test-ban ? n y Winning Vote
Class Name
democrat 8 59 200 Yes
republican 6 123 39 NA
aid-to-nicaraguan-contras ? n y Winning Vote
Class Name
democrat 4 45 218 Yes
republican 11 133 24 NA
mx-missile ? n y Winning Vote
Class Name
democrat 19 60 188 Yes
republican 3 146 19 NA
immigration ? n y Winning Vote
Class Name
democrat 4 139 124 Yes
republican 3 73 92 NA
synfuels-corporation-cutback ? n y Winning Vote
Class Name
democrat 12 126 129 No
republican 9 138 21 NA
education-spending ? n y Winning Vote
Class Name
democrat 18 213 36 No
republican 13 20 135 NA
superfund-right-to-sue ? n y Winning Vote
Class Name
democrat 15 179 73 Yes
republican 10 22 136 NA
crime ? n y Winning Vote
Class Name
democrat 10 167 90 Yes
republican 7 3 158 NA
duty-free-exports ? n y Winning Vote
Class Name
democrat 16 91 160 No
republican 12 142 14 NA
export-administration-act-south-africa ? n y Winning Vote
Class Name
democrat 82 12 173 Yes
republican 22 50 96 NA

From all the tables, we can see that democrats voting was generally much stronger, but partially also because there were more members of that party present. Most bills were voted in favor of (yes), and generally Democrats were more likely to get the favorable outcome.

Prepare The Data

Now that we know what to expect from our analysis and how our data spread is structured, we can prepare the data set for the model.

Since the data comes in yes/no format, we will need to convert this to numerical values so our Logistic Regression can work with the data. We will map ‘republican’ to 1 and ‘democrat’ to 0. Similarly for the data, we will map ‘yes’ to 1 and ‘no’ to 0. Since we do not want to count ‘?’ votes towards any single party, we will mark those votes with a value of 0.5, a neutral point.

# Prep data for Logistic Regression
X = data.copy()
X['Class Name'] = X['Class Name'].map({'republican':1, 'democrat':0})

for col in X.columns.drop('Class Name'):
    X[col] = X[col].map( 
                   {'y':1 ,'n':0, '?':0.5})

print(display(X.head()))
Class Name handicapped-infants water-project-cost-sharing adoption-of-the-budget-resolution physician-fee-freeze el-salvador-aid religious-groups-in-schools anti-satellite-test-ban aid-to-nicaraguan-contras mx-missile immigration synfuels-corporation-cutback education-spending superfund-right-to-sue crime duty-free-exports export-administration-act-south-africa
0 1 0.0 1.0 0.0 1.0 1.0 1.0 0.0 0.0 0.0 1.0 0.5 1.0 1.0 1.0 0.0 1.0
1 1 0.0 1.0 0.0 1.0 1.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 1.0 1.0 0.0 0.5
2 0 0.5 1.0 1.0 0.5 1.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 1.0 1.0 0.0 0.0
3 0 0.0 1.0 1.0 0.0 0.5 1.0 0.0 0.0 0.0 0.0 1.0 0.0 1.0 0.0 0.0 1.0
4 0 1.0 1.0 1.0 0.0 1.0 1.0 0.0 0.0 0.0 0.0 1.0 0.5 1.0 1.0 1.0 1.0 
None

Logistic Regression

First, the data will be split into training and testing sets, so we have can compare how well our model works after training it on the train set.

# Split data set into train and test sets, use standard 80-20 split
X_train, X_test, Y_train, Y_test = train_test_split(X.drop('Class Name',axis=1), X['Class Name'], train_size=0.8, test_size=0.2)

We will then build the Logistic Regression model. Since this model applies the Maximum Likelihood method, it is very powerful for calculating probabilities. It essentially will use these to figure out how to classify the data. This model will take the data and determine which party the individual belongs to based on their voting data. We will fit the data and then create a prediction list.

# Split data set into train and test sets, use standard 80-20 split
X_train, X_test, Y_train, Y_test = train_test_split(X.drop('Class Name',axis=1), X['Class Name'], train_size=0.8, test_size=0.2)

# Logistic Regression
log = LogisticRegression()
log.fit(X_train, Y_train)
predict = log.predict(X_test)

Let’s check how well our model works by finding its accuracy score. We will compare the predict set to the test set.

score = accuracy_score(Y_test, predict)
print(score)
0.9885057471264368

The model performs very well to this data set and has good accuracy. Over 90% accuracy means this Logistic Regression model fits the data set very strongly.

Additional Analysis - Confusion Matrix

To better understand how our model classified the data and its overall accuracy, we will look at a confusion matrix. This will show how many predictions are correct and incorrect, essentially giving us the prediction summary. It will provide data on the True Negatives, False Positives, False Negatives, and True Positives.

confusion = confusion_matrix(Y_test, predict)
confusion
array([[44,  1],
       [ 0, 42]])

This is the output array. Let’s graph this to visualize it better, for which we can use the ConfusionMatrixDisplay.

# Show confusion matrix on plot
cm_display = ConfusionMatrixDisplay(confusion_matrix = confusion, display_labels = [False, True])
cm_display.plot()
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x124eda510>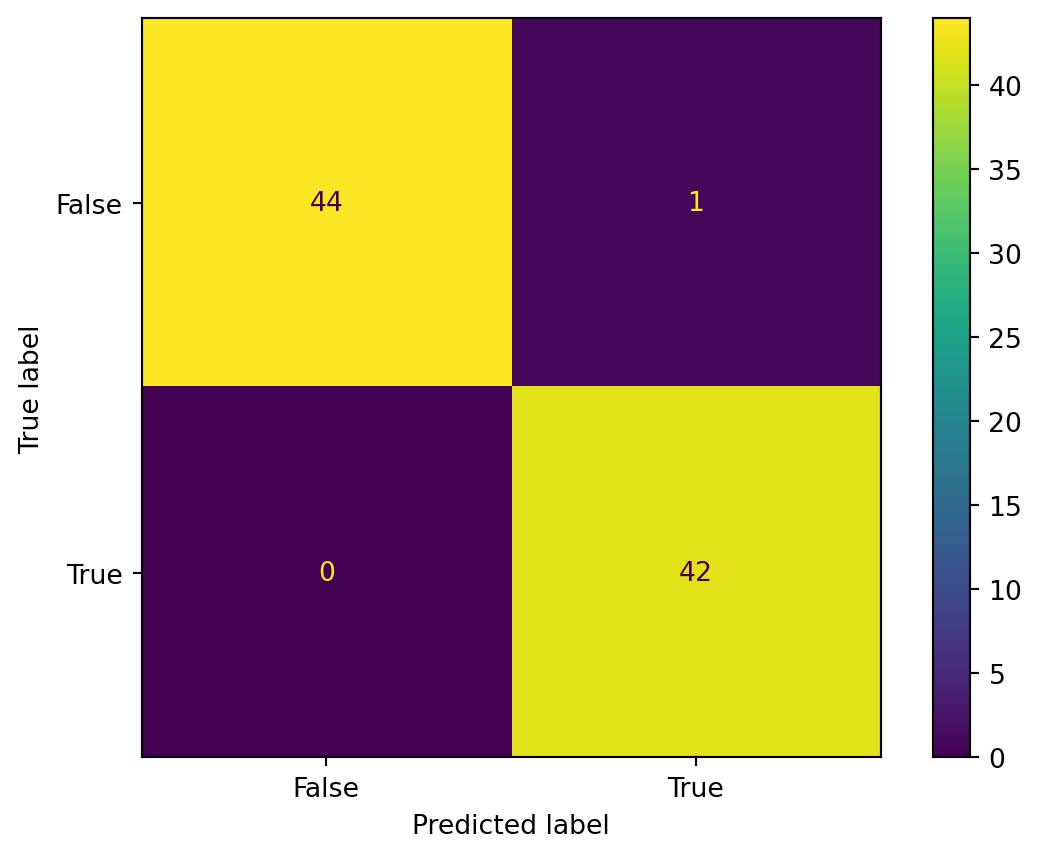

This lets us visualize how the Confusion matrix appears.